当隔壁家孩子还只能做着10以内的加法运算时,一个同龄的蒙氏宝宝已经开始做着千位数的乘除,玩着三项式的游戏,开始研究立体几何和平面。
今天小编和大家分享的正是蒙氏幼儿园培养幼儿数学心智的方法。我们的幼儿园也完全可以通过自制下文中的玩教具将蒙氏数学教学方法运用到实际中。
-
数学前预备期:感官学习
-
建立孩子数学感官的工作

数学,我们所生存的空间里无处不在。数学就像音乐,也是人类的一种与生俱来的本能,而教育的本质,就是帮助人类发展内在的这些能力。
数学具有内在的秩序性并力图展现最精确的结果,人对细节的敏感性(秩序感、准确性的强烈要求)在幼儿时期就存在,这与数学的特质是一致的。

1、借助实物化教具,把看似高深的数学概念简单化。
蒙特梭利创造了一套独特的数学教育方法,她把抽象的数学概念的学习“实物化”。
即给幼儿提供一套具体形象的实物教具,这些物化的教具为儿童提供了表象思维所需的具体形象,能很好的帮助幼儿学习数学。

2、注重以10为单位,让幼儿整体认知连续的数。
蒙氏数学教育有这样一个特点,无论什么知识,开始都是以10 为单位呈现出来的。一次就呈现给幼儿一组连续数。
例如,让幼儿认识10以内的数,不是先让幼儿认识“1”然后到“2”再到“10”,而是一次性地将数棒1—10全部呈现给幼儿,让幼儿看到的是一组连续数。
幼儿在摆弄这些数棒时,从短到长排列就会理解1—10的概念。

3、运用“从一般到个别”的教学方式,引入十、百、千位的加法运算。
蒙特梭利始终坚持按从一般到特殊的顺序呈现教学内容,也按照这种教学方法进行教学。都是以具体形象的教具为中介。

4、注重排序、分类、对应等概念的学习,注重发展幼儿数学思维。
蒙特梭利的数学教育是以感官教育为基础。强调事前准备是必须的,也就是说在进行数学教育之前先进行感觉教育,即对幼儿进行排序、对应、分类等数前学习。

5、注重数学在生活中的运用,注重教幼儿发现生活中的数学。
成功的数学教育应让幼儿体会数学是从人类实践中发展起来的,数学存在于现实生活中,让幼儿感知各种数学问题在现实生活中是怎样存在的。


数学前预备期:感官学习
研究发现,人出生后就对数的概念很敏感,这可以从幼儿的富有秩序感的动作中看出来,他们能够很自然地形成对周围环境的顺序性和对自己生活的秩序性。
这就是人类对数学这一概念的敏锐的感受性。这种感受性必须通过追求这样一个正确的程序才能获得,通常我们把这种状态称为“数学心智”。
蒙台梭利认为,要成为一连串的数学思考模式,就需要先把数学的内在组合与分解,也就是分开练习。
等到真正面对所谓有数字,有题目的数学时,才有解答的基础。

因此,在开始真正的数学学习前,需要经历一个漫长的感官学习期,称之为数学前的预备期。
这种观点,也与传统教学法中所提出的幼儿不应过早开展符号化学习,需要先通过具体的事物学习的观点不谋而合。
下面就来看一下,蒙特梭利是如何建立感官期到数学学习得内在联系,将数学学习贯穿整个学习生涯始终。
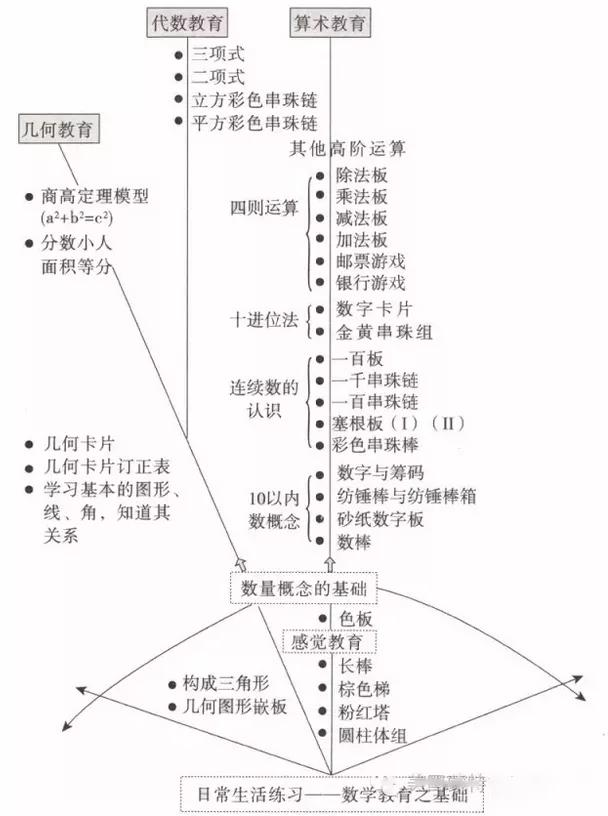
从上图可以看出,感官教育是整个蒙氏数学教育的根基所在。在进行数学学习前,我们通过大量的感官工作来帮助幼儿建立内在的数学心智。
蒙特梭利的感觉教育包括视觉、触觉、听觉、嗅觉和味觉等感官的训练。
视觉训练在于帮助幼儿提高度量的视知觉,鉴别大小、高低、粗细、长短、形状、颜色及不同的几何形体。

触觉练习则是帮助幼儿辨别物体是光滑还是粗糙,辨别温度的冷热,辨别物体的轻重、大小、厚薄。
听觉训练是要使幼儿习惯于区分声音的差别,使他们在听声的训练中不仅能够分辨音色、音高,还能培养初步的审美和鉴赏能力。
嗅觉和味觉的训练则是注重提高幼儿嗅觉和味觉的灵敏度。


建立孩子数学感官的工作
我们将利于数学学习的感官工作归类为配对、分类和序列三大类工作,这三类工作也经常以组合的形式出现。
下面,我们就来具体的看一下,这三类工作是如何开展的。
-
1、配对(P):建立等于的概念,通过一对一的经验,帮助幼儿发现等值性的关系。
从找到另一只相同的小袜子开始让孩子感受到这就是所谓的一一对应的关系是不是感觉很神奇呢?

从实物和实物的配对开始,可以逐渐发展到等比例实物和平面的配对,再到平面和平面的配对,再到平面和同类平面的配对。


这个顺序和日后学习立体几何到平面几何的顺序完全相同,也是建立数与量概念的基础。

(实物和实物的配对)
运用生活中一些空的瓶罐,将盖子与瓶身分开,再让孩子自己组合,也是很好的配对材料。

除此之外,老师们还可以用小木棒和硬纸板自己制作玩教具。

螺丝和螺丝帽也是很好的配对教具组合。

(实物和平面的配对)

(纸片上的字母和木架上的字母配对)

(动物与图片的配对)
也可以自制蒙氏教具:将各种瓶盖的大小画下来,再让孩子将瓶盖与纸上的形状重合。

同样,可以将孩子常用或熟悉的小物品的轮廓画出来做配对。


(平面和平面配对)





(数与量的一一对应)
-
2、分类(S):建立包含的概念,按照东西归类,让孩子了解部分与全体的关系,培养幼儿的类比与推理能力。
通过早期视觉分辨不同颜色的训练,孩子逐渐具有了区分相同事物和不同事物的能力。

这种区分,逐渐培养孩子认识事物内在区别和联系的能力,帮助孩子认识整体和局部。

为日后的乘除运算能力打下基础,培养孩子发展出事物内在逻辑联系的概括能力。


通过对同类色的排列和大小的区分,孩子已经在感官层面具备了掌握二项式(a+b)^2=a^2+b^2+2ab和三项式的能力。

通过对同类色的排列和大小的区分,孩子已经在感官层面具备了掌握二项式(a+b)^2=a^2+b^2+2ab和三项式的能力。


从整体到局部,这就是分数运算的开始。

-
3、序列(G):建立大于小于的概念,让孩子了解大小的概念,也是未来加减运算的基础。
从帮助孩子视觉发展的渐进色悬挂物开始,已经开始培养孩子的序列感。



从色彩的渐进到嵌套玩具,从无标记的长棒到表示数列大小关系的数棒,从最初的加减到几何平方,孩子内在数学的秩序感一步步被打开。


幼儿的秩序感与生俱来,他们喜欢反复操作这些秩序感很强的工作,这也是培养专注力最好的方法。


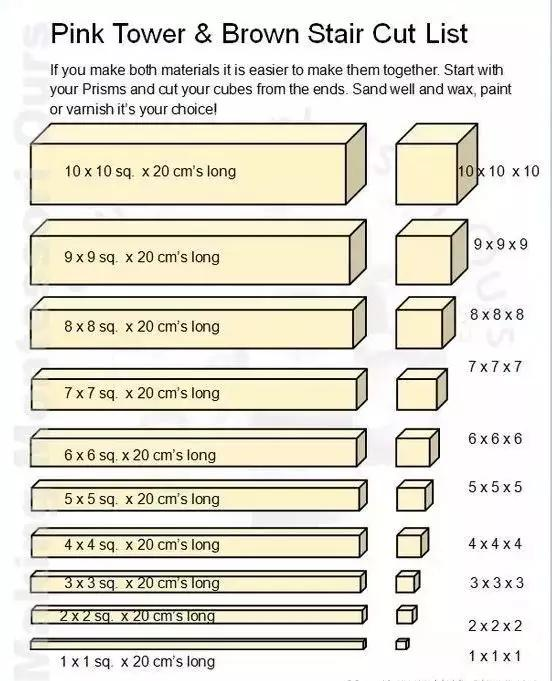
长棒代表长短,粉红塔是体积关系,综合体延伸出面积,所有的蒙氏教具都是相互关联层层递进,拥有内在的逻辑与联系。



每一个工作都有教育意义,所以蒙氏教室里没有玩具只有教具。


从色彩的渐进到嵌套玩具,从无标记的长棒到表示数列大小关系的数棒,从最初的加减到几何平方,孩子内在数学的秩序感一步步被打开。



让孩子从实物中感受到数的连续性,在大量的感官工作后,孩子进入了真正的数学学习。


从具体到抽象,这个时期孩子已经可以自如进行抽象数字的加减乘除。


———>>
写在后面的话
<<———
与传统数学教学法不同,蒙特梭利数学教育旨在为儿童奠定直观认知基础,发展其数理逻辑和空间智能,培养对数学的兴趣。
数学不在是纸上的数字,而是幼儿从内在建立起的秩序和对数与量的感知。数学,不是在教室的考卷上,而是融合在生活里,流淌在血液中。

延伸阅读:蒙台梭利 | 我们可以为孩子提供什么样有意义的室内环境?
蒙台梭利 | 20种日常生活中的前导性工作,促进孩子自我发展









